https://www.acmicpc.net/problem/1018
1018번: 체스판 다시 칠하기
첫째 줄에 N과 M이 주어진다. N과 M은 8보다 크거나 같고, 50보다 작거나 같은 자연수이다. 둘째 줄부터 N개의 줄에는 보드의 각 행의 상태가 주어진다. B는 검은색이며, W는 흰색이다.
www.acmicpc.net
브루트 포스를 사용하는 문제였다.
브루트 포스 알고리즘은 어렵지 않아서 이 것을 이용해야 하는 것을 알면 쉬운데,
그게 아닐 경우 높은 확률로 시간 초과에 걸리기 때문에
항상 BFS, DFS인지를 고민하는데 시간을 많이 쓰게 된다.
전형적인 문제의 형식이 있는 것 같다고도 느껴져서 한 번 몰아서 풀어보면 좋을 것 같다.
핵심 변수
char expectedColor : 시작점의 값('B' or 'W')을 저장하는 변수
int cnt : 각 격자에 대한 탐색에서 다시 칠해야 하는 정사각형의 개수
int answer : 모든 격자에 대해 다시 칠해야 하는 정사각형의 최소 개수
알고리즘 방식
1. 8x8의 격자를 만들 수 있는 위치를 1행 1열부터 찾는다.
예를 들어 N = 10, M = 11이라면, 행으로는 3행까지 열로는 4열까지를 시작점으로 하는 8x8 격자를 만들 수 있고,
이 때는 3 * 4 = 12개의 8x8 격자를 만들 수 있다.

2. 2중 for문을 통해 생성된 격자의 모든 위치에 차례대로 접근한다.
이 과정에서 시작점의 값을 expectedColor에 저장하고,
a. 접근 위치의 값이 expectedColor와 다르면 cnt++

b. 다음 위치로 이동할 때 그 값을 뒤집는다. (뒤집는다 : 'B'는 'W' 반대로, 'W'는 'B')
이때, 다음 위치에서 행이 바뀐다면 그 값을 뒤집지 않는다.

3. 먼저 이해하고 가야 될 부분이 있다.
예를 들어, expectedColor = 'B'일 때, 모든 격자를 탐색한 결과 cnt = 30이라면,
동일한 격자에서 expectedColor = 'W'일 때, 모든 격자를 탐색한 결과 cnt = 64 - 30이다.
(값이 지속적으로 정확히 반대이므로, 둘의 합은 64(모든 칸의 개수)이다.
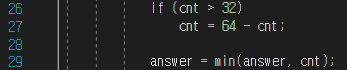
그렇기 때문에, cnt의 값이 32보다 크다면 expectedColor를 반대로 했을 때, 그 값은 32보다 작다는 이야기이고
즉, cnt의 값이 32보다 크다면 다시 칠해야 하는 정사각형의 개수는 expectedColor를 반대로 했을 때의 cnt이다.
따라서 cnt의 값이 32보다 크면 이를 64에서 뺀 값을 cnt에 다시 저장한다.
그 후, 그 값이 이전의 격자들에서 다시 칠해야 하는 정사각형의 최소 개수보다 작은 지를 판단하여 answer에 저장한다.
소스코드
#include <iostream>
#define min(a, b) a < b ? a : b
using namespace std;
int N, M;
char board[51][51];
int answer = 64;
int BruteForce() {
for (int i = 0; i < N - 7; i++) {
for (int j = 0; j < M - 7; j++) {
char expectedColor;
int cnt = 0;
expectedColor = board[i][j];
for (int x = i; x < i + 8; x++) {
for (int y = j; y < j + 8; y++) {
if (expectedColor != board[x][y])
cnt++;
if (y != j + 7)
expectedColor = expectedColor == 'B' ? 'W' : 'B';
}
}
if (cnt > 32)
cnt = 64 - cnt;
answer = min(answer, cnt);
}
}
return answer;
}
int main(void) {
ios::sync_with_stdio(false);
cin.tie(NULL);
cin >> N >> M;
for (int i = 0; i < N; i++) {
cin >> board[i];
}
cout << BruteForce();
}
'알고리즘 > C++' 카테고리의 다른 글
| [백준] 2217 - 로프 by C++ (0) | 2022.11.08 |
|---|---|
| [백준] 1629 곱셈 by C++ (0) | 2022.11.04 |
| [백준] 2146번 다리 만들기 by C++ (0) | 2022.09.13 |
| [백준] 11729번 하노이 탑 (0) | 2021.03.18 |
| [백준] 2573번 빙산 (0) | 2021.03.17 |




댓글